- Sample Size Calculation Software Machine
- Sample Size Calculation Software Mac
- Sample Size Calculation Software Macros
- Sample Size Calculation Software Macro
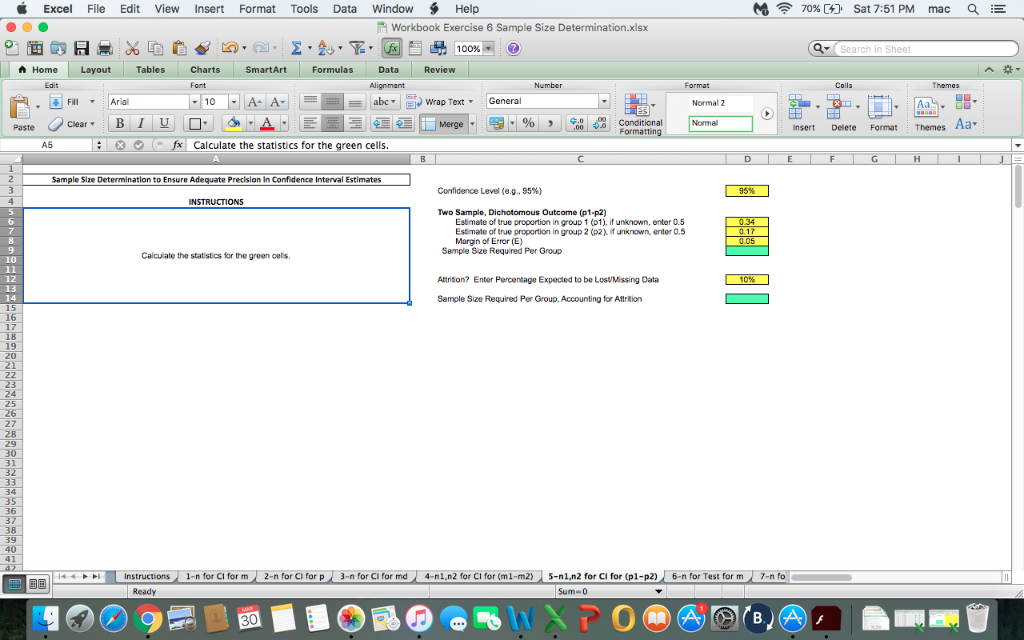
The number of observations made by each subject. The sample size calculations are derived from Power Analysis and Sample Size (PASS) software where the alpha and minimum required power is fixed at 0.05 and higher than 0.80 respectively. A discussion on how to use these tables for determining sample sizes required for each of the. The sample size calculator supports experiments in which one is gathering data on a single sample in order to compare it to a general population or known reference value (one-sample), as well as ones where a control group is compared to one or more treatment groups (two-sample, k-sample) in order to detect differences between them.
1-sample z-test for a population proportion
1-Stage Freedom analysis
2-sample t-test for summary data
2-sample z-test to compare sample proportion
2-Stage surveys for demonstration of freedom
Analyse test repeatability
Analyse two-stage prevalence data
Analysis of 2-stage freedom survey data
Analysis of simple 2-stage freedom survey
Bioequivalence analysis - two-period, two-treatment crossover trial
Calculate Cluster-level sensitivity and specificity for range of sample sizes and cut-points for given cluster size and imperfect tests
Calculate confidence limits for a sample proportion
Calculate sample sizes for 2-stage freedom survey where individual cluster details are available
Calculate sample sizes for 2-stage freedom survey where individual cluster details are NOT available
Calculate sample sizes for 2-stage freedom survey with fixed cluster-level sensitivity
Calculate test Sensitivity and Specificity and ROC curves
Capture-Recapture analysis
Chi-squared test for contingency table from original data
Chi-squared test for homogeneity of a sample
Chi-squared test for r x c contingency table
Chi-squared test for trend
Cluster-level sensitivity and specificity with variable cut-points
Compare prevalence values
Compare two tests
Complex 2-stage risk-based surveillance - calculation of surveillance sample size
Complex 2-stage risk-based surveillance - calculation of surveillance sensitivity
Complex 2-stage risk-based surveillance - calculation of surveillance sensitivity based on herd testing data
Complex risk-based surveillance - calculation of surveillance sample size
Complex risk-based surveillance - calculation of surveillance sensitivity
Confidence of population freedom (NPV) for a surveillance system
Confidence of population freedom for multiple time periods
Contact
Design prevalence required to achieve target population (cluster or system) sensitivity
Diagnostic test evaluation and comparison
Estimate 95% confidence limits for a median
Estimate alpha and beta Parameters for Beta distributions from count data
Estimate confidence limits for a mean
Estimate parameters for multiple Beta probability distributions or summarise distributions for specified parameters
Estimated true prevalence and predictive values from survey testing
Estimated true prevalence using one test with a Gibbs sampler
Estimated true prevalence using two tests with a Gibbs sampler
Estimating prevalence
Estimation of alpha and beta parameters for prior Beta distributions
'EUFMD - Demonstration of FMD freedom': 2-stage risk-based surveillance with 1 herd-level risk factor, 1 animal-level risk factor and multiple surveillance components
FreeCalc: Analyse results of freedom testing
FreeCalc: Calculate sample size for freedom testing with imperfect tests
Get P and critical values for the Chi-squared distribution
Get P and critical values for the F distribution
Get P and critical values for the normal distribution
Get P and critical values for the t distribution
Glossary
HerdPlus utilities
HerdPlus: Calculate SeH and SpH for a single herd
HerdPlus: SeH and SpH comparison for varying herd sizes
HerdPlus: SeH and SpH for listed herd sizes and optimised sample sizes
HerdPlus: SeH and SpH for optimised sample sizes for range of herd sizes
HerdPlus: SeH and SpH for range of sample sizes and cut-points for given herd size
HerdPlus: SeH and SpH for varying sample sizes
HerdPlus: SeH for fixed sample size and cut-point
HerdPlus: SeH for optimised sampling strategy
HerdPlus: SeH for varying design prevalence
Home
Likelihood ratios and probability of infection in a tested individual
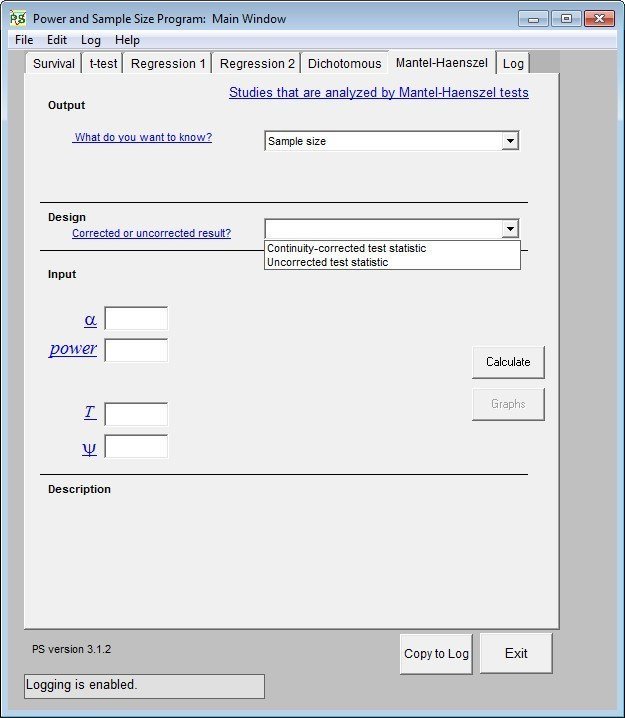
Mantel-Haenszel chi-square test for stratified 2 by 2 tables
McNemar's chi-squared test for association of paired counts
Numbers of false positives to a test
One-sample test to compare sample mean or median to population estimate
Paired t-test or Wilcoxon signed rank test on numeric data
Pooled Prevalence
Pooled Prevalence Calculator - Demonstration analyses
Pooled Prevalence Calculator - Demonstration analyses - 1
Pooled Prevalence Calculator - Demonstration analyses - 2
Pooled Prevalence Calculator - Demonstration analyses - 3
Pooled Prevalence Calculator - Demonstration analyses - 4
Pooled Prevalence Calculator - Demonstration analyses - 5
Pooled Prevalence Calculator - Demonstration analyses - 6
Pooled Prevalence Calculator - Demonstration analyses - 7
Pooled Prevalence Calculator - Demonstration analyses - 8
Pooled Prevalence Calculator - Demonstration analyses - 9
Pooled Prevalence Calculator - Demonstration analyses - 10
Pooled Prevalence Calculator - Demonstration analyses - 11
Pooled Prevalence Calculator - Demonstration analyses - 12
Pooled Prevalence Calculator - Demonstration analyses - 13
Pooled Prevalence Calculator - Demonstration analyses - 14
Pooled Prevalence Calculator - Demonstration analyses - 15
Pooled Prevalence Calculator - Demonstration analyses - 16
Pooled Prevalence Calculator - Demonstration analyses - 17
Pooled prevalence for fixed pool size and perfect tests
Pooled prevalence for fixed pool size and tests with known sensitivity and specificity
Pooled prevalence for fixed pool size and tests with uncertain sensitivity and specificity
Pooled prevalence for variable pool size and perfect tests
Pooled prevalence using a Gibbs sampler
Population (or cluster) sensitivity for varying unit sensitivity
Population level (or herd, flock, cluster, or other grouping) sensitivity
Population or cluster level sensitivity using pooled sampling
Positive and Negative Predictive Values for a test
Probability of infection in a test-negative sample
Random Geographic Coordinates Sampling
Random Number Sampling
Random sampling from a sampling frame
Random sampling from populations
Random sampling of animals
References
Risk-based surveillance
Sample size calculation for fixed pool size and perfect tests
Sample size calculation for fixed pool size and uncertain sensitivity and specificity
Sample size calculations
Sample size for a case-control study
Sample size for a cohort study
Sample size for demonstration of freedom (detection of disease) using pooled testing
Sample Size for survival analysis to compare median times since last outbreak
Sample size required to achieve target confidence of freedom
Sample size to achieve specified population level (or herd, flock, cluster, etc) sensitivity
Sample size to detect a significant difference between 2 means with equal sample sizes and variances
Sample size to detect a significant difference between 2 means with unequal sample sizes and variances
Sample size to detect a significant difference between 2 proportions
Sample size to estimate a proportion or apparent prevalence with specified precision
Sample size to estimate a single mean with specified precision
Sample size to estimate a true prevalence with an imperfect test
Sample size to estimate a true prevalence with an imperfect test
Simple 2-stage risk-based surveillance - calculation of sample size
Simple 2-stage risk-based surveillance - calculation of surveillance sensitivity
Simple 2-stage risk-based surveillance - calculation of surveillance sensitivity based on herd testing data
Simple risk-based surveillance - calculation of minimum detectable prevalence
Simple risk-based surveillance - calculation of sample size
Simple risk-based surveillance - calculation of surveillance sensitivity
Simple risk-based surveillance with differential sensitivity - calculation of sample size with two sensitivity groups
Simple risk-based surveillance with differential sensitivity - calculation of surveillance sensitivity
Simulate sampling for fixed pool size and assumed known test sensitivity and specificity
Simulate sampling for fixed pool size and assumed perfect test
Simulate sampling for fixed pool size and uncertain test sensitivity and specificity
Simulate sampling for variable pool sizes
Simulated true prevalence estimates from survey testing with an imperfect test
Statistical analysis of numeric data
Stochastic analysis of 2-stage freedom survey data
Summarise Beta probability distributions for specified alpha and beta parameters
Summarise Binomial probability distributions for specified sample size and probability
Summarise categorical or continuous data
Summarise continuous data (ungrouped)
Summarise continuous data by single grouping variable
Summarise measures of association from a 2x2 table
Summarise Pert probability distributions for specified minimum, mode and maximum values
Summarise probability distributions
Survey Toolbox for livestock diseases
Survival analysis of herd incidence data
Test evaluation against a gold standard
User guide - Home
User guide 1 - Introduction
User guide 2 - Overview
User guide 3 - Bayesian vs frequentist methods
User guide 4 - Pooled prevalence for fixed pool size and perfect tests
User guide 5 - Pooled prevalence for fixed pool size and tests with known sensitivity and specificity
User guide 6 - Pooled prevalence for fixed pool size and tests with uncertain sensitivity and specificity
User guide 7 - Pooled prevalence for variable pool size and perfect tests
User guide 8 - Pooled prevalence using a Gibbs sampler
User guide 9 - Estimated true prevalence using one test with a Gibbs sampler
User guide 10 - Estimated true prevalence using two tests with a Gibbs sampler
User guide 11 - Estimation of alpha and beta parameters for prior Beta distributions and summarisation of Beta distributions for specified alpha and beta parameters
User guide 12 - Sample size for fixed pool size and perfect test
User guide 13 - Sample size for fixed pool size and known test sensitivity and specificity
User guide 14 - Sample size for fixed pool size and uncertain test sensitivity and specificity
User guide 15 - Simulate sampling for fixed pool size
User guide 16 - Simulate sampling for variable pool sizes
User guide 17 - Important Assumptions
User guide 18 - Pooled prevalence estimates are biased!
If 50% of all the people in a population of 20000 people drink coffee in the morning, and if you were repeat the survey of 377 people ('Did you drink coffee this morning?')many times, then 95% of the time, your survey would find that between 45% and 55% of the people in your sample answered 'Yes'.
The remaining 5% of the time, or for 1 in 20 survey questions, you would expect the survey response to more than the margin of error away from the true answer.
When you survey a sample of the population, you don't know that you've found the correct answer, but you do know that there's a 95% chance that you're within the margin of error of the correct answer.
Try changing your sample size and watch what happens to the alternate scenarios.That tells you what happens if you don't use the recommended sample size, and how M.O.E and confidence level (that 95%) are related.
To learn more if you're a beginner, read Basic Statistics: A Modern Approach and The Cartoon Guide to Statistics. Otherwise, look at themore advanced books.In terms of the numbers you selected above, the sample size n and margin of error
Sample Size Calculation Software Machine
 E are given by
E are given by | x | = | Z(c/100)2r(100-r) |
| n | = | N x/((N-1)E2 + x) |
| E | = | Sqrt[(N - n)x/n(N-1)] |
Sample Size Calculation Software Mac
is the fraction ofresponses that you are interested in, and Z(cSample Size Calculation Software Macros
 /100) isthe criticalvalue for the confidence level c.
/100) isthe criticalvalue for the confidence level c.If you'd like to see how we perform the calculation, view the pagesource. This calculation is based on the Normaldistribution, and assumes you have more than about 30 samples.
About Response distribution